Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and buildHere is the graph of y = sin x The height of the curve at every point is the line value of the sine In the language of functions, y = sin x is an odd function It is symmetrical with respect to the origin sin (−x) = −sin x y = cos x is an even function The independent variable x is the radian measure x may be any real number We may imagine the unit circle rolled out, in bothFeb 23, 17 · I dont know how to type cos^2(x) sin^2(x) into matlab I think it is cos(x)^2 sin(x)^2 Also I know the interval is typed out 2*pi, 2*pi} but I dont understand what the question means by saying using 100 points in the domain
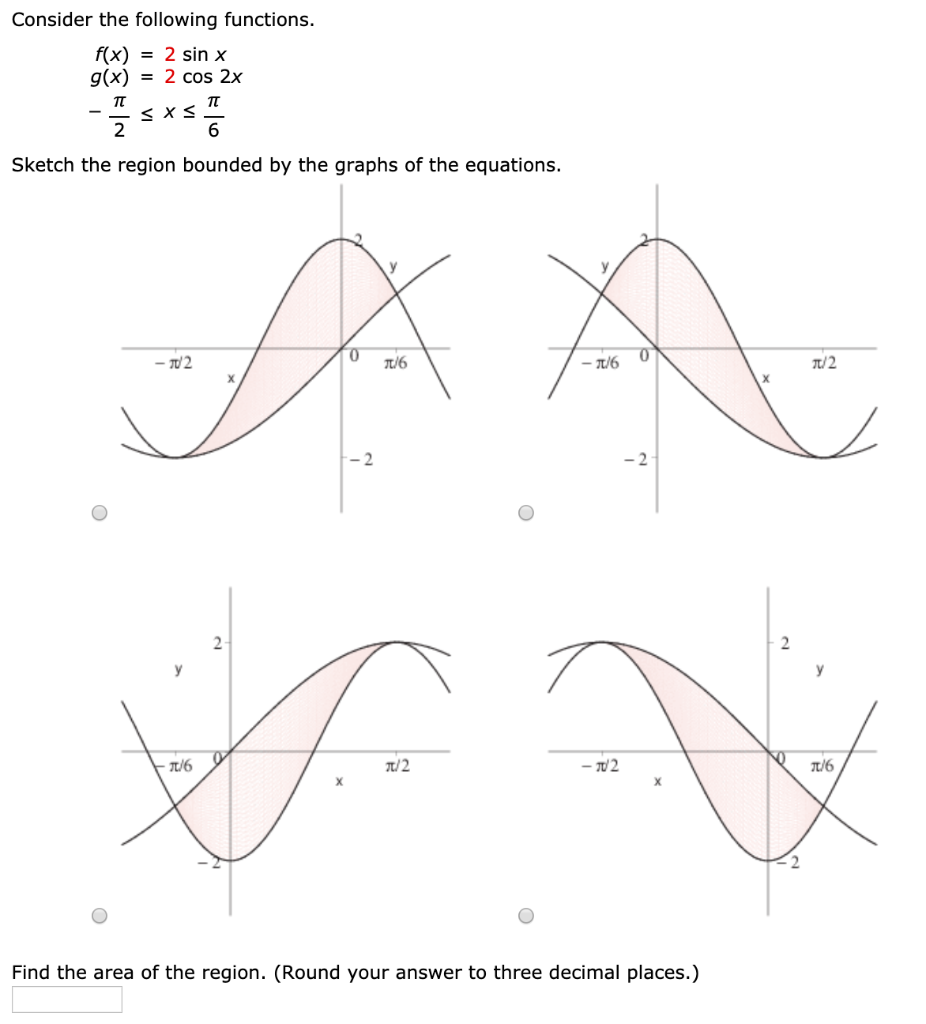
Solved Consider The Following Functions F X 2 Sin X G Chegg Com
Graph the function f(x)=cos x 2
Graph the function f(x)=cos x 2-The values of x corresponding to the points at which the graph of the function f (x) = x − 2 sin x has a horizontal tangent has to be determined For a function f (x) the slope of the tangent atRight the equation of the function f of X graphed below so we have this clearly periodic function so immediately you might say well this is either going to be a sine function or cosine function but its midline and its amplitude are not just the plain vanilla sine or cosine function and we can see that right over here the midline is halfway between the maximum point and the minimum point the




The Maximum Ordinate Of A Point On The Graph Of The Function F X Sin X 1 Cos X Maths Continuity And Differentiability Meritnation Com
This problem has been solved!Graph of the function y = 2 cos(x) Example 4 Find the range and the period of the function y = 2 cos(x) and graph it Solution to Example 4 Comparing the given function = 2 cos(x) and the basic cosine function y = cos(x), there is a vertical stretching of a factor of 2 and there is also a reflection on the x axis because of the minus in 2Graph two full periods of the function f (x) = cos (6x) and state the amplitude and period Enter the exact answers For the number 7, either choose from the dropdown menu or type in Pi (with a capital P) Amplitude A Period P = Select the correct graph of the function f (x) = cos (6x)
Calculus (a) By graphing the function f (x) = (cos 2x − cos x)/x2 and zooming in toward the point where the graph crosses the yaxis, estimate the value of lim x → 0 f (x) (b) Check your answer in part (a) by evaluating f (x) for valuesMar 07, · The graph of y = 10 cos x, which we learned about in the last section, sine and cosine curves, is as follows 05π π 15π 2π 5 10 5 10 x y Open image in a new page The graph of `y=10cos(x)` for `0 ≤ x ≤ 2pi`Function Grapher is a full featured Graphing Utility that supports graphing up to 5 functions together You can also save your work as a URL (website link) Usage To plot a function just type it into the function box Use "x" as the variable like this Examples sin(x) 2x−3;
Click here👆to get an answer to your question ️ The graph of the function cos xcos (x 2) cos^2(x 1) is a(a) By graphing the function $ f(x) = (\cos 2x \cos x)/x^2 $ and zooming in toward the point where the graph crosses the $ y $ axis , estimate the value of $ \displaystyle \lim_{x \to 0}f(x) $ (b) Check your answer in part (a) by evaluating $ f(x) $ for values of $ x $ that approach 0Trigonometry Graph f (x)=cos (x) f (x) = cos (x) f ( x) = cos ( x) Use the form acos(bx−c) d a cos ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = 1 a = 1 b = 1 b = 1 c = 0 c = 0 d = 0 d = 0 Find the amplitude a a




Show That Int 0 2 Pi Cos 2 X Dx Int 0 2 Pi Sin 2 X Dx Mathematics Stack Exchange



Example 13 Find Area Bounded By Y Cos X X 0 2pi Examples
Nov 30, 15 · The graph of f(x), a trigonometric function, and the graph of g(x) = c intersect at n points over the interval 0 rate of change Joe is investigating the rate of change of the function y=cos x on the interval xE0,2π He notices that the graph of y=cos x passes through the xDifficult to answer completely We will give sufficient conditions only 2May 28, 21 · For example, f(x) = sin(x), B = 1, so the period is 2π ,which we knew If f(x) = sin(2x), then B = 2, so the period is π and the graph is compressed If f(x) = sin(x 2), then B = 1 2, so the period is 4π and the graph is stretched Notice in Figure 2




Graphs Of The Sine And Cosine Function Precalculus Ii




Rd Sharma Solutions For Class 11 Chapter 6 Graphs Of Trigonometric Functions Exercise 6 2 Avail Free Pdf
Cosine f x x( ) cos= Since the period of the cosine function is 2π, we will graph the function on the interval 0, 2π The rest of the graph is made up of repetitions of this portion Key points in graphing cosine functions are obtained by dividing the period into four equal parts (Assuming no vertical shifting and no xaxis reflection)Beyond simple math and grouping (like "(x2)(x4)"), there are some functions you can use as well Look below to see them all They are mostly standard functions written as you might expect You can also use "pi" and "e" as their respective constants Please note You should not use fractional exponentsGoal Given a function f(x), write it as a linear combination of cosines and sines, eg f(x) = a 0a 1cos(x) a 2cos(2x) ··· b 1sin(x) b 2sin(2x) ··· = a 0 X∞ n=1 (a ncos(nx) b nsin(nx)) Important Questions 1 Which f have such a Fourierseriesexpansion?




Drill For Exam Graph Cie



Graphs Of Sine And Cosine Ppt Download
Graph the following function {eq}f(x) = 2x^2 11x 5 {/eq} Quadratic Function A quadratic function, on being graphed, gives us a parabola This parabola could beY=cosx y'=D(cosx) y'=sinx*D(x) y'={x/x}sinx The question is, is y=cosx differentiable everywhere, y is differentiable everywhere if and only if the function y' is continuous everywhere The function y' comprises of a sinusoidal funcFrom this, we can see that to attain g(x), we need to compress f(x) horizontally by a factor of 2, vertically stretch f(x) by a scale factor of 3, and translate the resulting function 1 unit upward Let's slowly graph g(x) by applying these transformations Let's start by horizontally compressing f(x) by a scale factor of 2
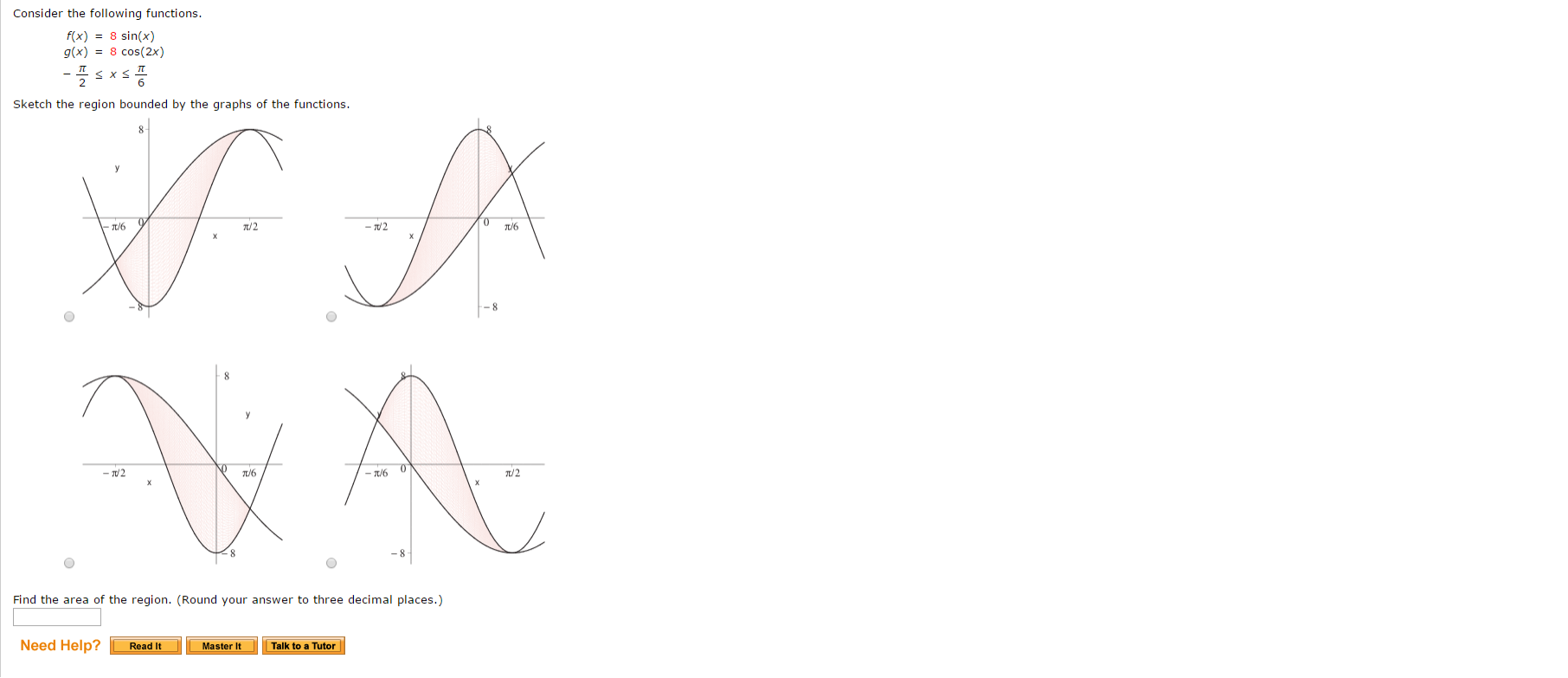



Consider The Following Functions F X 8 Sin X Chegg Com



Rates Of Change Of Sin X And Cos X Geogebra
Jul 05, 16 · Let $f(x)=\cos(x)\cos(x2)\cos^2(x1)$ \begin{align} f'(x)&=\sin x\cos(x2)\cos x\sin(x2)2\cos(x1)\sin(x1)\\ &=\sin(2x2)\sin(2x2)\\ &=0 \end{align} So it is a constant function, ie, a horizontal straight lineTo draw the graph of the cosine function divide the unit circle and xaxis of a Cartesian coordinate system the same way as when drawing the sine function The abscissas of the ending points of arcs x , of the unit circle, are now the ordinates of the corresponding points P ( x , cos x ) of the graph, as shown in the figure belowThere is no answer available Request an answer from our educators and we will get to it right away!




The Maximum Ordinate Of A Point On The Graph Of The Function F X Sin X 1 Cos X Maths Continuity And Differentiability Meritnation Com




If 2 Cos X Sin X 3 Then The Range Of The Function F
Graph f (x)=2cos (x) f (x) = 2 − cos (x) f ( x) = 2 cos ( x) Rewrite the expression as −cos(x) 2 cos ( x) 2 −cos(x) 2 cos ( x) 2 Use the form acos(bx−c) d a cos ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = −1 a =1) right a units, up b units 2) right a units, down b units 3) left a units, up b units 4) left a units, down b units 12 Which transformation could be used to make theCos(x^2) (x−3)(x3) Zooming and Recentering To zoom, use the



Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions



Sketching The Graph Of Cos 2x Youtube
Let f(x) be a function of period 2π such that f(x) = x 2 over the interval 0 < x < 2π a) Sketch a graph of f(x) in the interval 0 < x < 4π b) Show that the Fourier series for f(x) in the interval 0 < x < 2π is π 2 − sinx 1 2 sin2x 1 3 sin3x c) By giving an appropriate value to x, show that π 4 = 1− 1 3 1 5 − 1 7 1 9 −Calculus Using the first and second derivative, sketch the graph of f(x) = sin(x) cos(x)Textbook solution for Calculus Early Transcendentals 8th Edition James Stewart Chapter 1 Problem 15RE We have stepbystep solutions for your textbooks written by Bartleby experts!




The Range Of Function F X Cos X



Draw The Graph Of The Function F X M A Xdot Sinx Cos2x X In 0
Which describes the behavior of the function f(x) = tan^1(x) C x to infinity, f(x) to pi/2 Find the value of Sin^1(tan pi/4) D pi/2 Find the value of tan(sin^1(1/2)) C sqrt3/3 Write the equation for the inverse of the function y = cos^1(x pi) C y = pi cosx Write the equation for the inverse of the function y = Arcsin 3xFunction to plot, specified as a function handle to a named or anonymous function Specify a function of the form y = f(x) The function must accept a vector input argument and return a vector output argument of the same size Use array operators instead of matrix operators for the best performance For example, use * (times) instead ofFree functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy
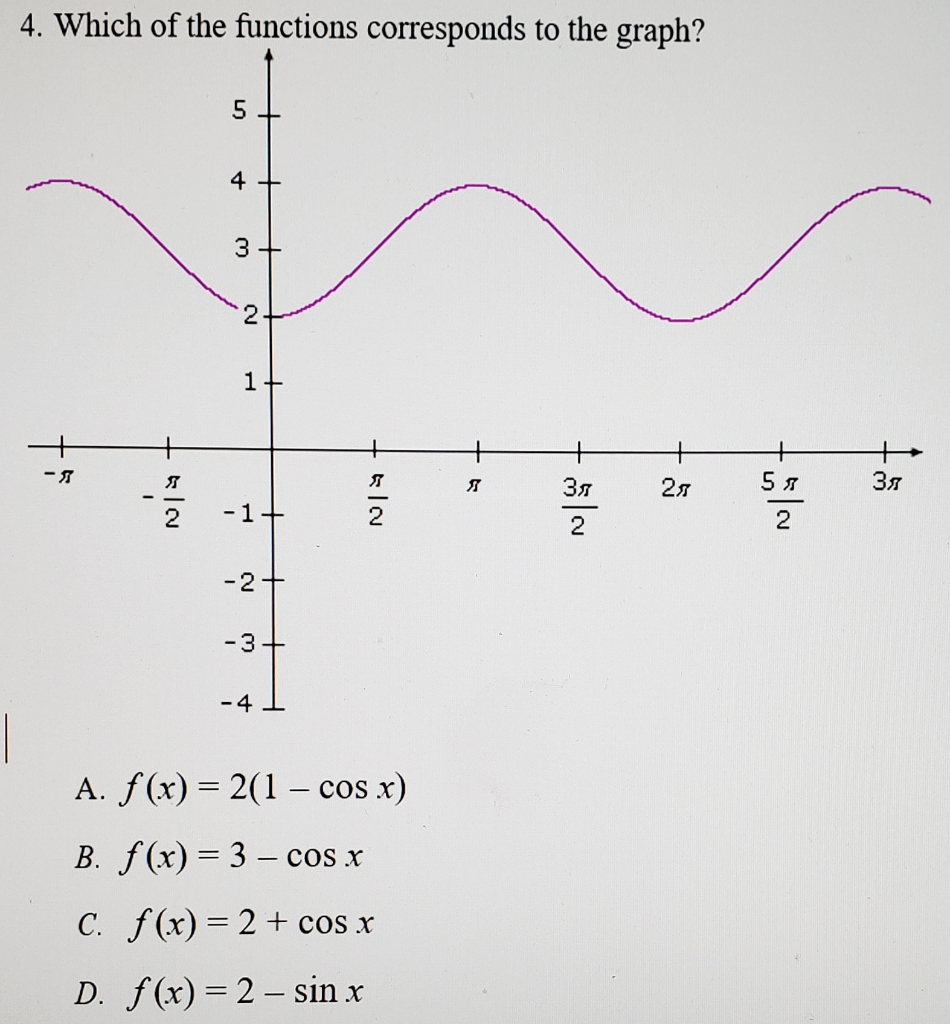



Solved 4 Which Of The Functions Corresponds To The Graph Chegg Com




Series Fourier Series Graham S Mcdonald A Self Contained Tutorial Module For Learning The Technique Of Fourier Series Analysis Pdf Free Download
11 Given the parent function p(x) cosx, which phrase best describes the transformation used to obtain the graph of g(x) cos(x a) b, if a and b are positive constants?Graph the function {eq}f(x) = \sin x \cos(\frac{x}{2}) {/eq} Find the period of f(x) based on the graph Confirm the period of f(X) by solving algebraicallyApr 22, 18 · To graph f (x) = 1 cos(x), start working on it's Parent Function f (x) = cos(x) first Make a table of values for f (x) = cos(x) and f (x) = 1 cos(x) For x, consider the values 0, π 2,π, 3π 2 and 2π If you examine Col 4 and Col 5, you see that the difference is 1 Graph of y = f (x) = cos (x)




Show That The Function Defined By F X Cos X 2 Is A Continuous




Example 48 Show That F X Tan 1 Sin X Cos X Is Always
Mar 06, 19 · sin (x π/2 ) = cos x y = cos x graph is the graph we get after shifting y = sin x to π/2 units to the left Period of the cosine function is 2π Max value of Graph Min value of the graph 1 at 0, 4π 1 at 2π There are a few similarities between the sine and cosine graphs, They are Both have the same curve which is shifted along theNow we'll repeat the process for the basic cosine function )f x( ) =cos( x The domain of this function is (−∞, ∞) and the range is 1, 1 Again, we typically graph just one complete period of the graph, that is on the interval 0, 2 π Here is the table of values for )f x( ) =cos( x x 0 6 π 4 π 3 π 2 π 3 2π 4 3π 6 5π π 6//googl/JQ8NysThe Graph of the Function f(x) = cos(x)




Find The Points On The Curve Y Cos X 2 Sin X At Which The Tangent Is Horizontal Youtube



Draw The Graph Of Y Cos X X In 0 2pi Where Repres
Jun 17, 21 · Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeMay 22, 18 · Please Subscribe here, thank you!!!The graph of y=sin(x) is like a wave that forever oscillates between 1 and 1, in a shape that repeats itself every 2π units Specifically, this means that the domain of sin(x) is all real numbers, and the range is 1,1 See how we find the graph of y=sin(x) using the unitcircle definition of sin(x)




Answered A By Graphing The Function F X Bartleby
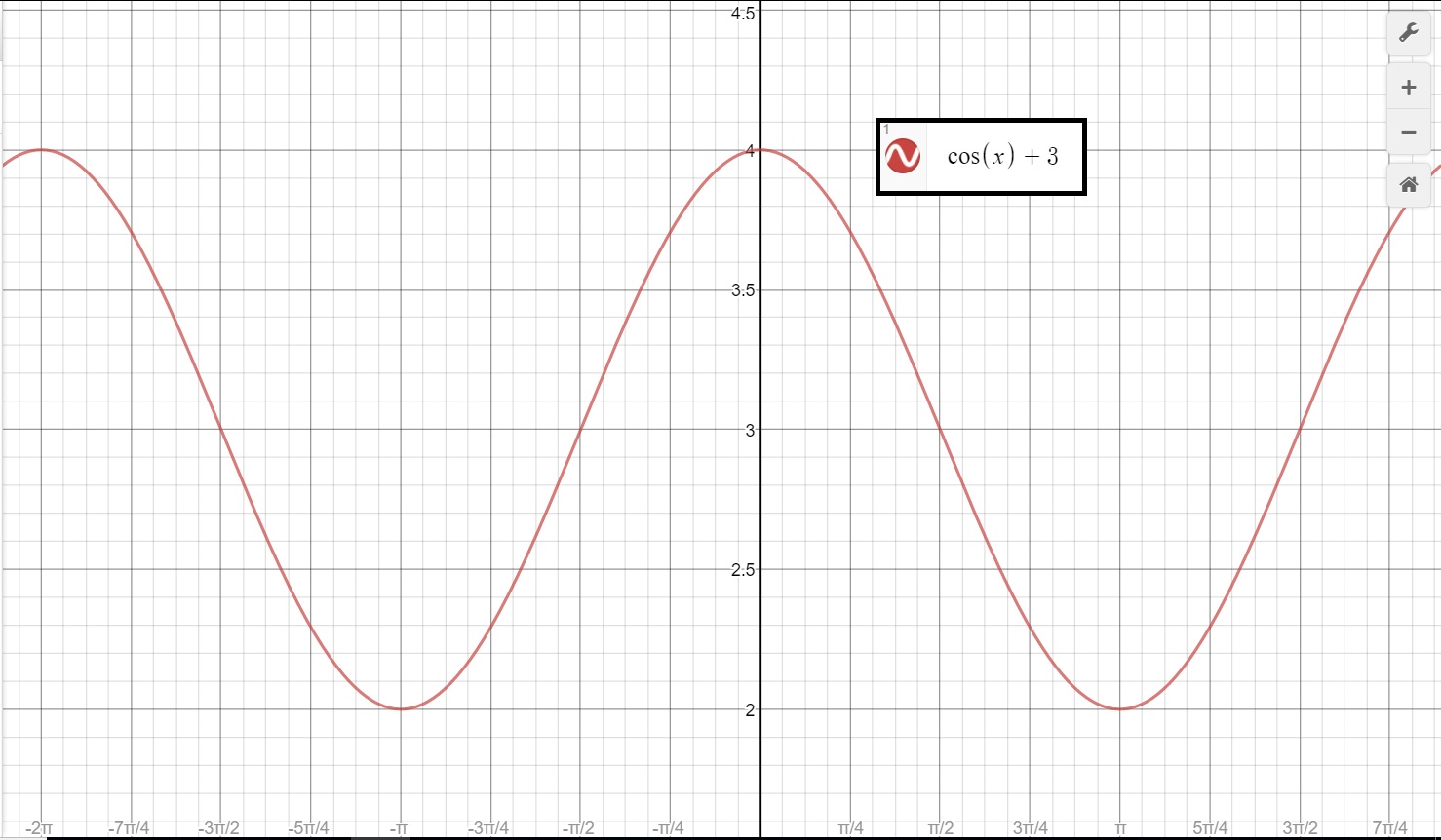



How Do You Graph Y Cosx 3 Socratic
How can we plot the following three functions f(x) = sin(x) k(x) = cos(x) u(x) = x² for x ∈ 0,1 on a single plot with the help of TikZ?SOLVEDGraph f (x)=2^ {\cos x} (a) Is the function Problem Let f ( x) = − cos x and g ( x) = sin x (a) What is Uh oh!In mathematics, the graph of a function is the set of ordered pairs (,), where () =In the common case where and () are real numbers, these pairs are Cartesian coordinates of points in twodimensional space and thus form a subset of this plane In the case of functions of two variables, that is functions whose domain consists of pairs (x, y), the graph usually refers to the set of




Ex 5 1 32 Show That F X Cos X Is Continuous Class 12




The Number Of Points Where F X Sin X Cosx Where Denotes The Greatest Integer Fun Youtube
Dec 21, · 24 Derivatives of Trigonometric functions One of the most important types of motion in physics is simple harmonic motion, which is associated with such systems as an object with mass oscillating on a spring Simple harmonic motion can be described by using either sine or cosine functionsSee the answer Graph two full periods of the function f (x)=cos (6x) and state the amplitude and period Enter the exact answers For the number π, either choose π from the dropdown menu or type in Pi (with a capital P) Amplitude A= Number Period P= Preview Change entry modeF (x) =Cos (π/4) =1/√2 f (x) = Cos (π/4) = 1/√2 = f (x) Here, we need to note that ( π/4) lies in the 4th quadrant Hence, all, cos values are positive in 4th quadrant Similarly, graph of sin (x) is symmetric about the origin Here you get the sign of output varies with sign of input value x




Answers
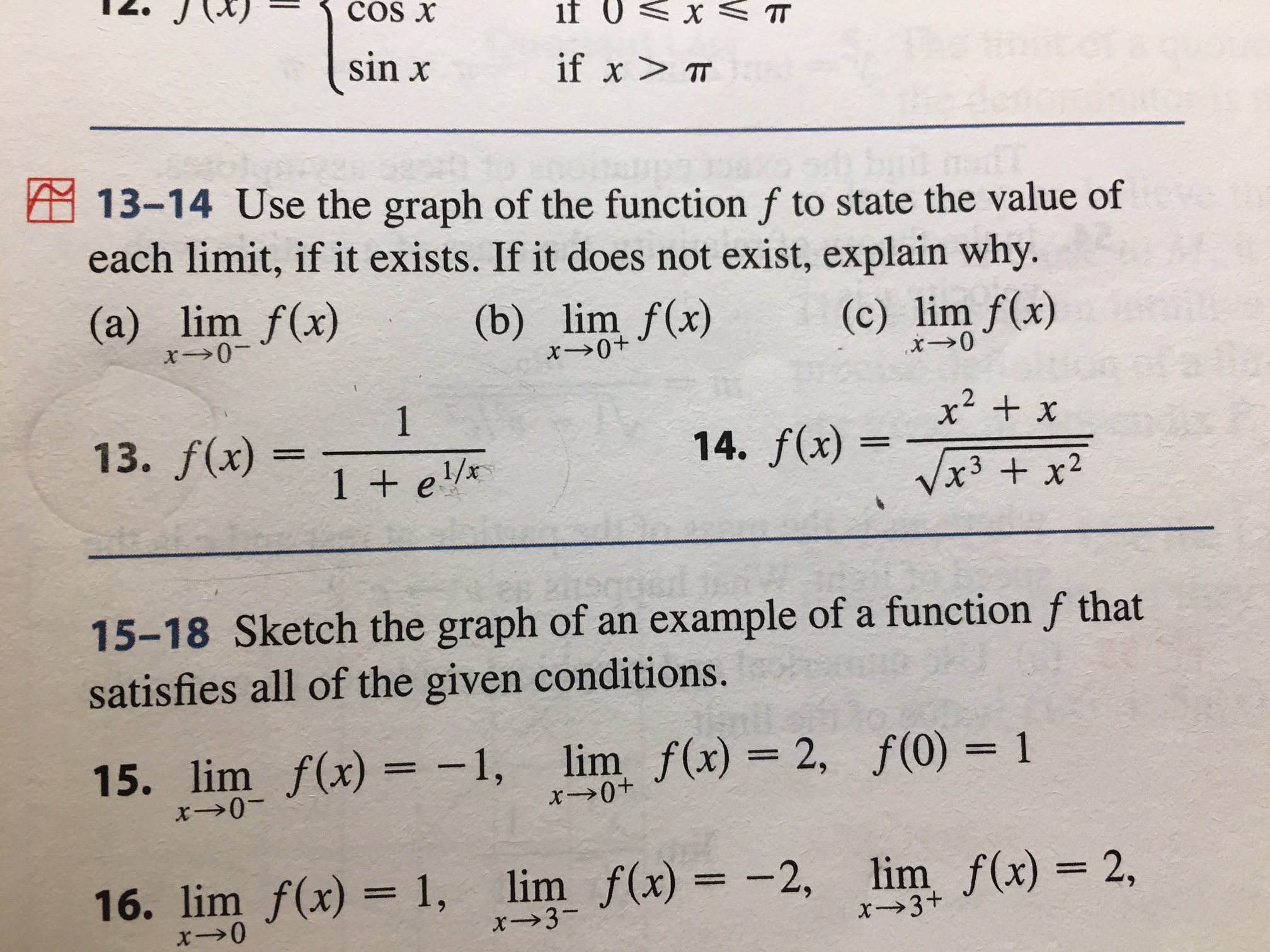



Answered 12 Jx Cos X 1f X Tt Sin X If X T Bartleby



Solved A Estimate The Area Under The Graph Of F X 10 Cos X From X 0 To X Jr Z Using Four Approximating Rectangles And Right Endpoints R Course Hero




What Is The Range Of Cos X




Transformation Of Cos X To Sin X Via Cos X Frac Pi 2 Sin X Mathematics Stack Exchange




Intersection Points Of Y Sin X And Y Cos X Video Khan Academy
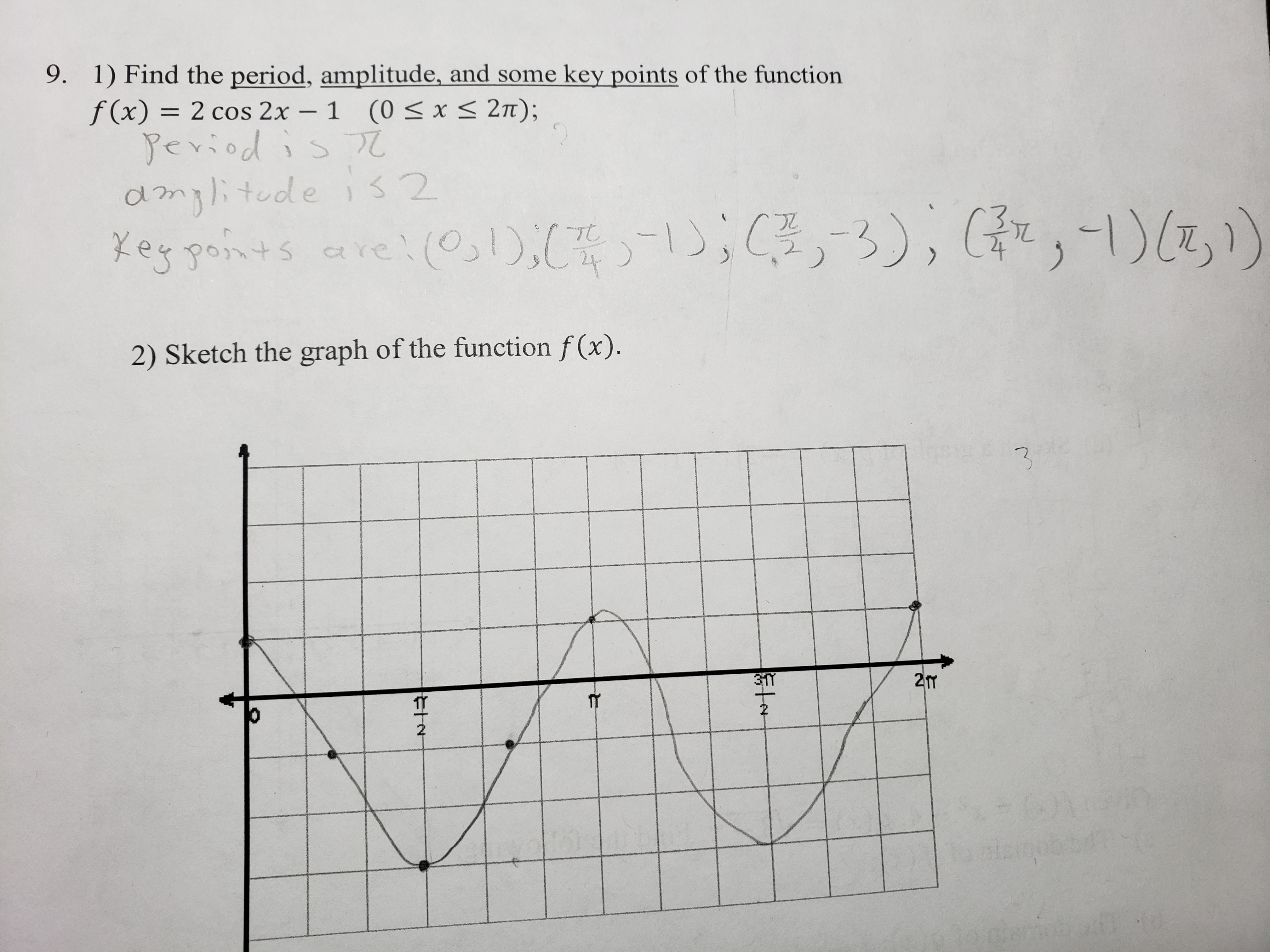



Answered 9 1 Find The Period Amplitude And Bartleby
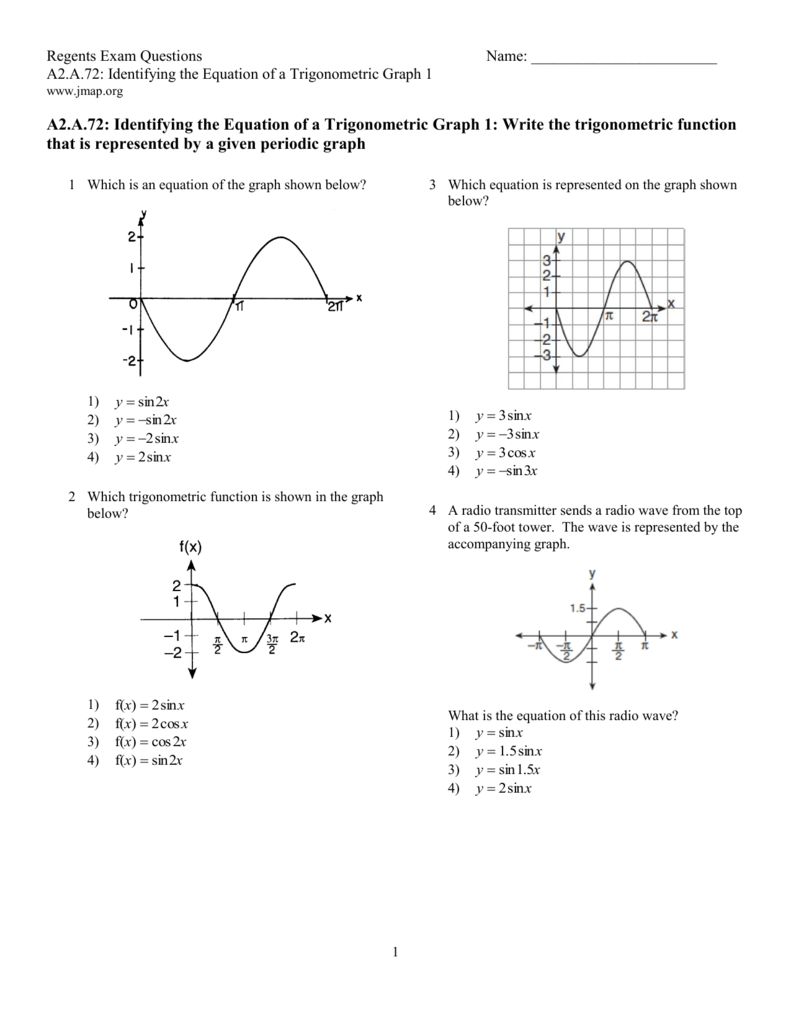



A 72 Identifying The Equation Of A Trigonometric Graph 1 Write




Derivatives Of Sin X And Cos X Video Khan Academy




Linear Approximation And Differentials In Calculus Owlcation




Derivative Rules For Trigonometric Functions




Solved Function F X First Second Derivatives F X F X Given F X Cos 2x F X Sin 2x Cos 2x 2 F X Tsi Q




Find The Values Of X For Which F X Sqrt Sin X Cos X Is Def




Ex 5 1 32 Show That F X Cos X Is Continuous Class 12




Trigonometry Reciprocal Identities Expii



Transformation Of Graphs Ppt Download




Is The Function F X Cos X Even Odd Or Neither Socratic




What Are Periodic Functions Expii



How Do You Graph The Derivative Of F X Cos X Socratic




Let The Function F X Have The Form Fx Acos X C To Produce A Graph That Matches The One Shown Brainly Com




Pp 6 If F I 1 1 F X Cos X Fin 0 8 0 6 0 4 2 Chegg Com




Answered 3 3x 1 34 F 33 F X 5x X2 36 Bartleby




The Range Of The Function F X 2 Sin X 3 Cos X Is Youtube




Even Or Odd F X Cos 3x Sin 2x Trigonometric Functions Youtube



What Is The Fourier Series Of F X Cos X If 0 X P Quora
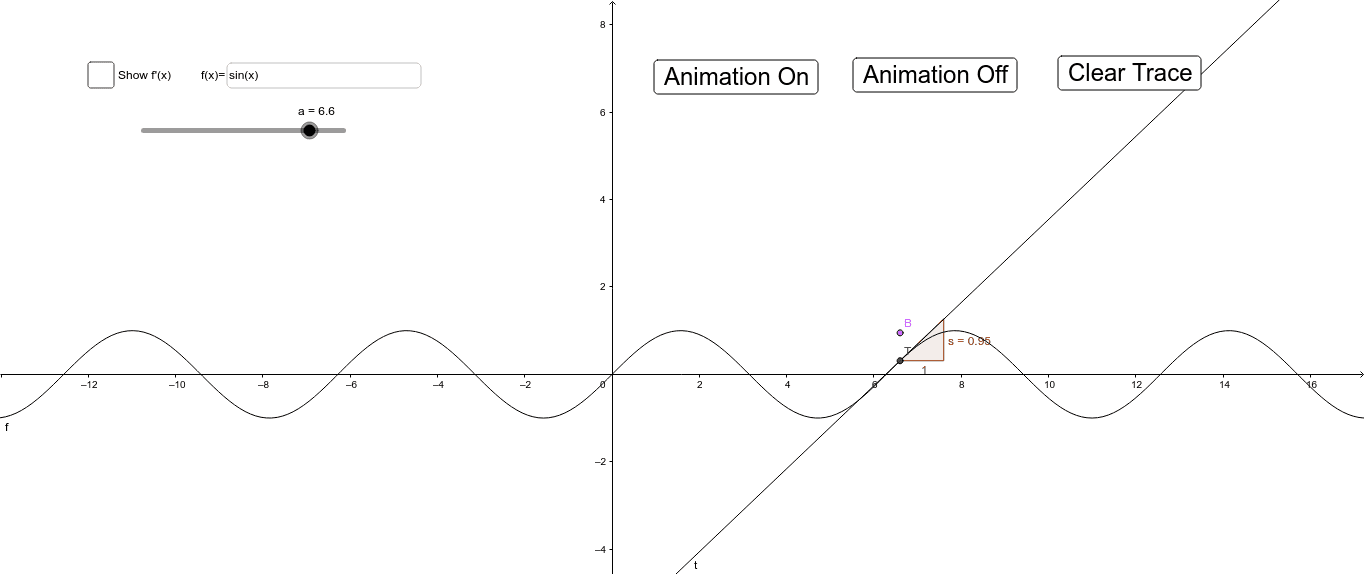



The Derivative Of F X Sin X Is G X Cos X Geogebra
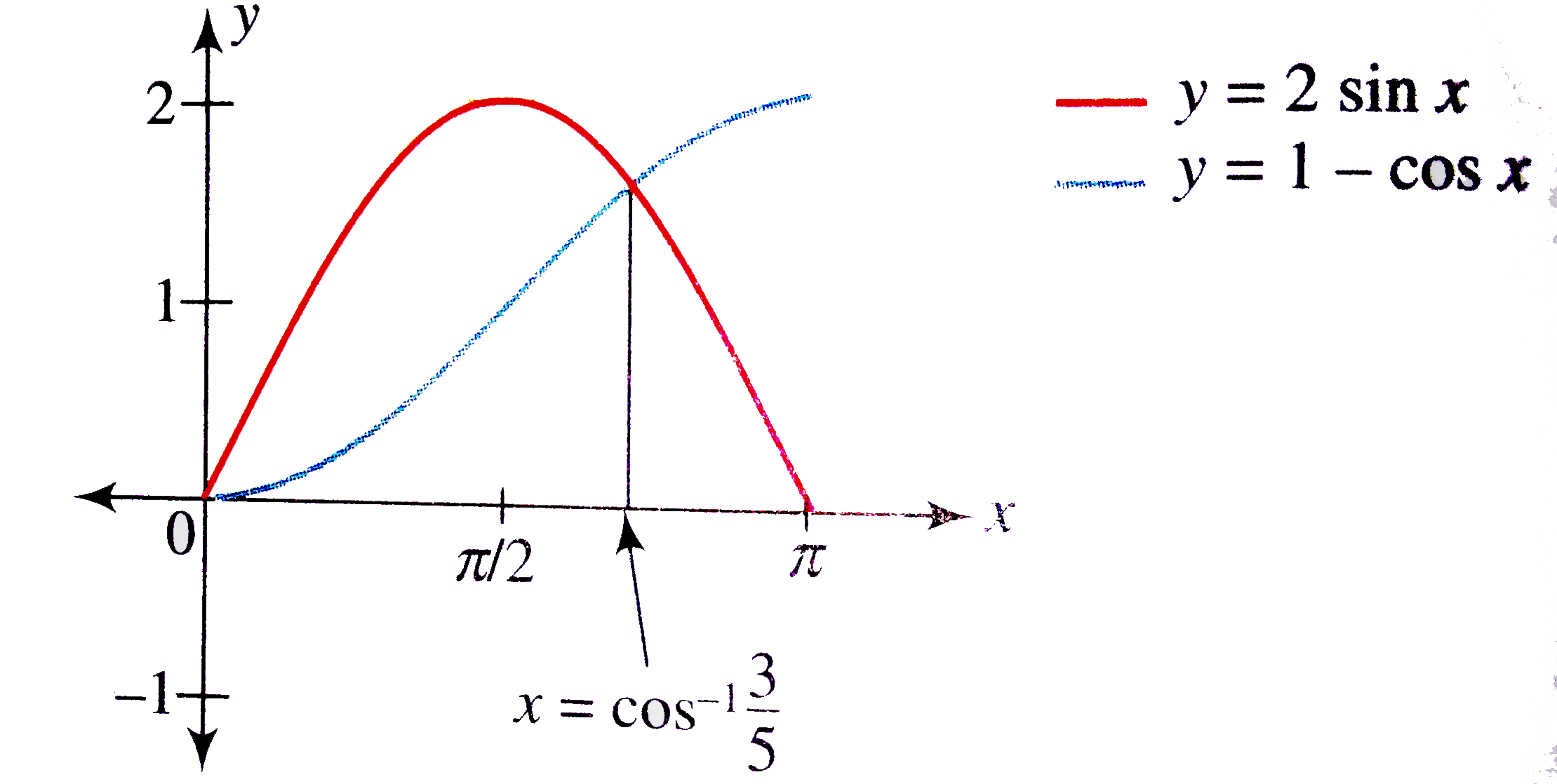



Draw The Graph Of F X Maximum 2 Sin X 1 Cos X X In 0



Solved A Estimate The Area Under The Graph Of F X 10 Cos X From X 0 To X Jr Z Using Four Approximating Rectangles And Right Endpoints R Course Hero




Solved Consider The Following Functions F X 2 Sin X G Chegg Com




Notes On Topics Of Algebra Notes




How To Solve F X 3sinx
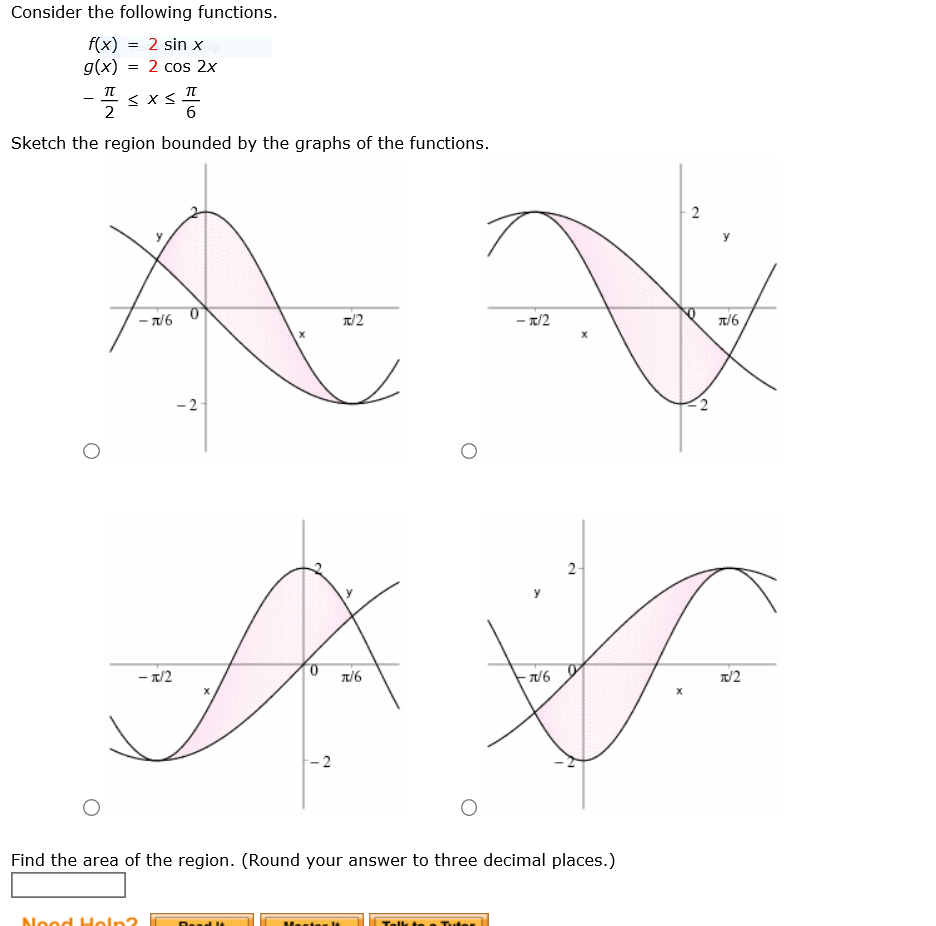



Consider The Following Functions F X 2 Sin X Chegg Com
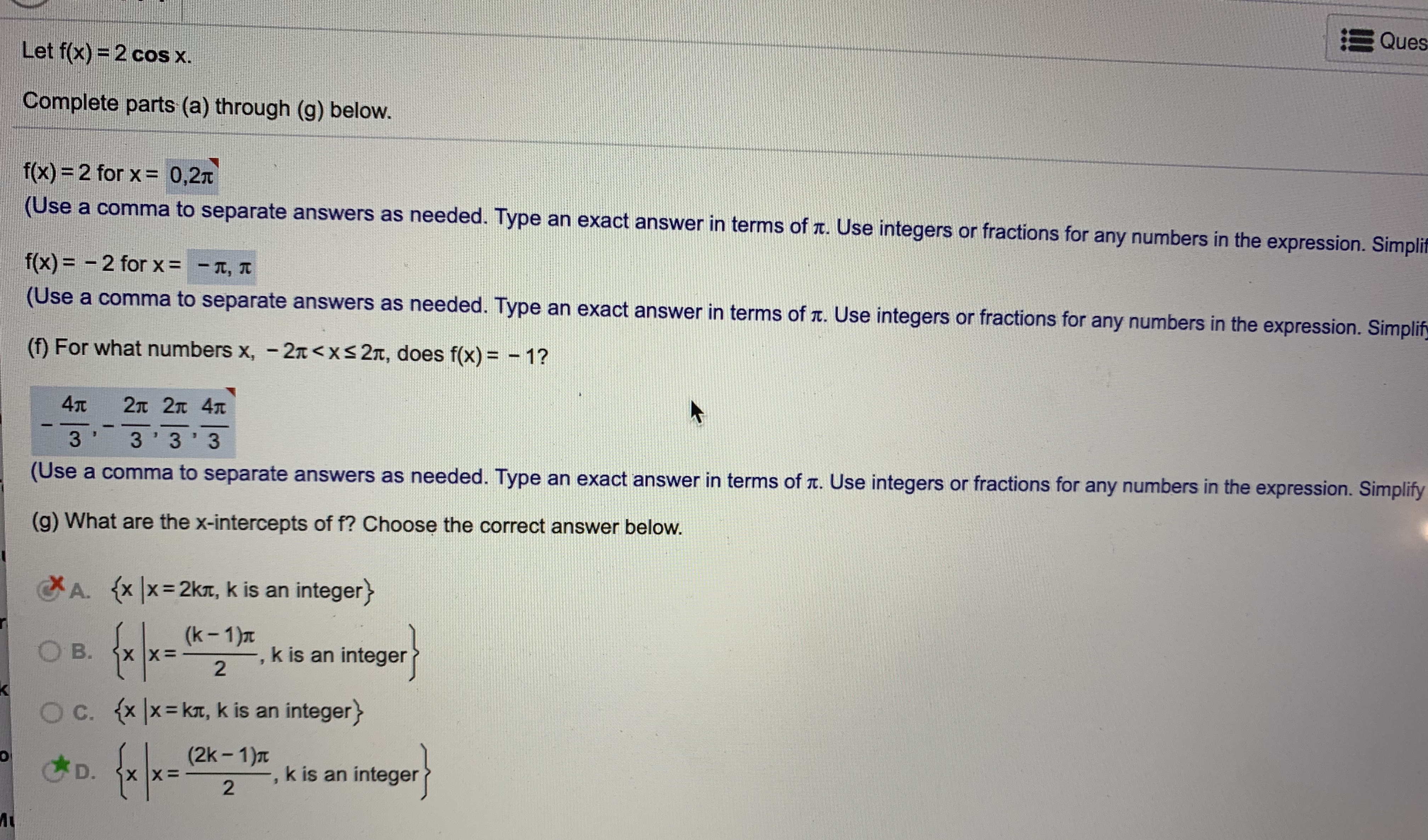



Answered Let F X 2 Cos X Complete Parts A Bartleby




Gdc Set Up Ensure That Your Calculator Is In Degree Mode And That You Know How To Adjust The V Window Of Your Graphs Before Doing These Trigonometry Graphs Ppt Download




Find The Range Of F X 2sin X 3cos X 5
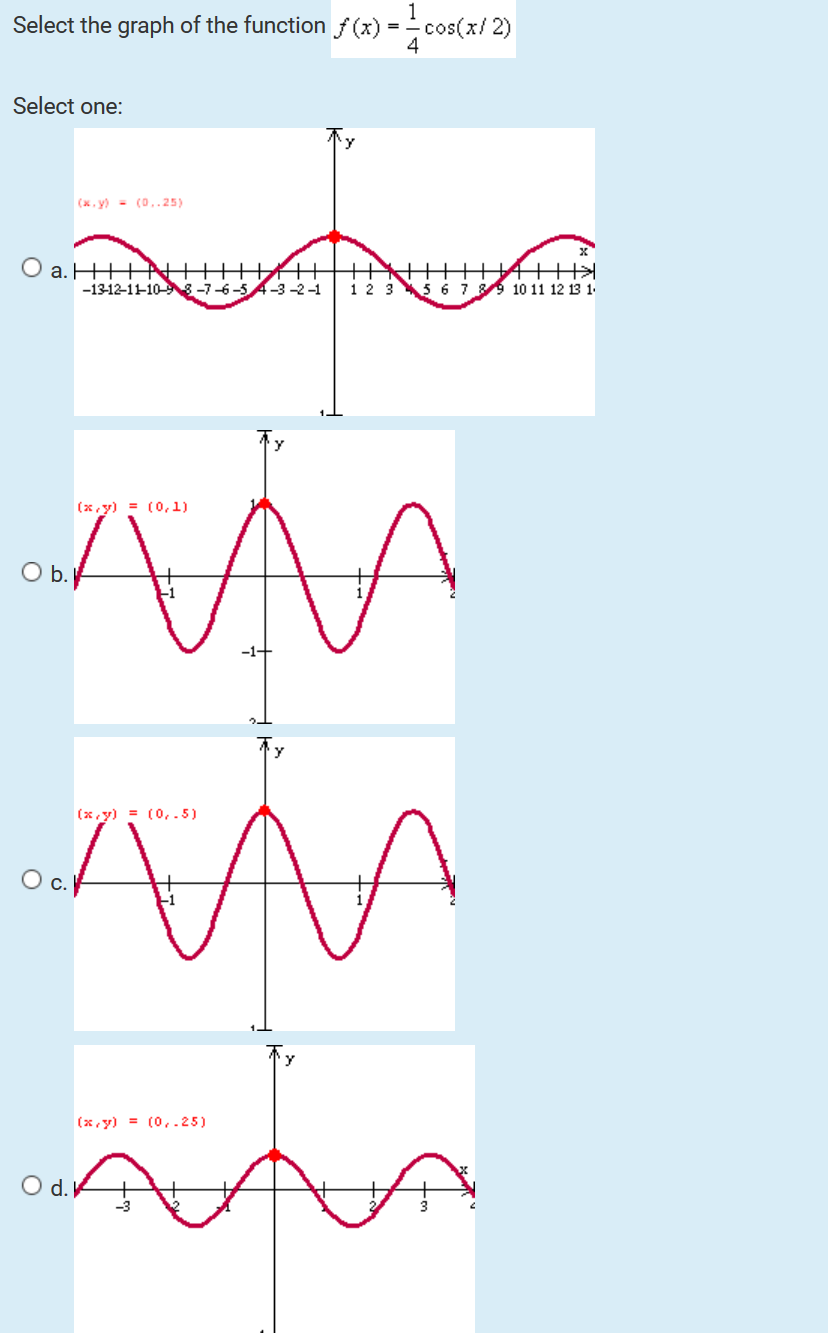



Select The Graph Of The Function F X 3 Cos X 2 Chegg Com
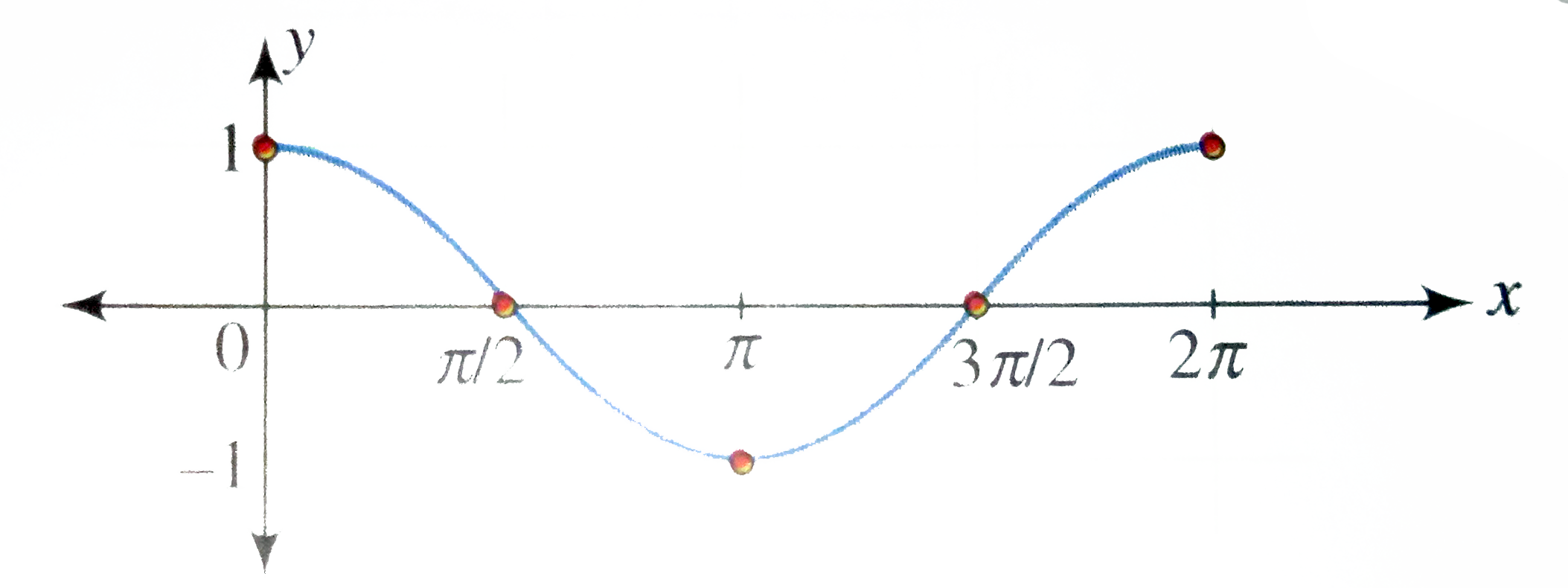



Draw The Graph Of Y Cos X X In 0 2pi Where Repres




Answered 1 For The Function F X X 1 E A Bartleby




Graph The Function F X Cos 2x 1 Brainly Com
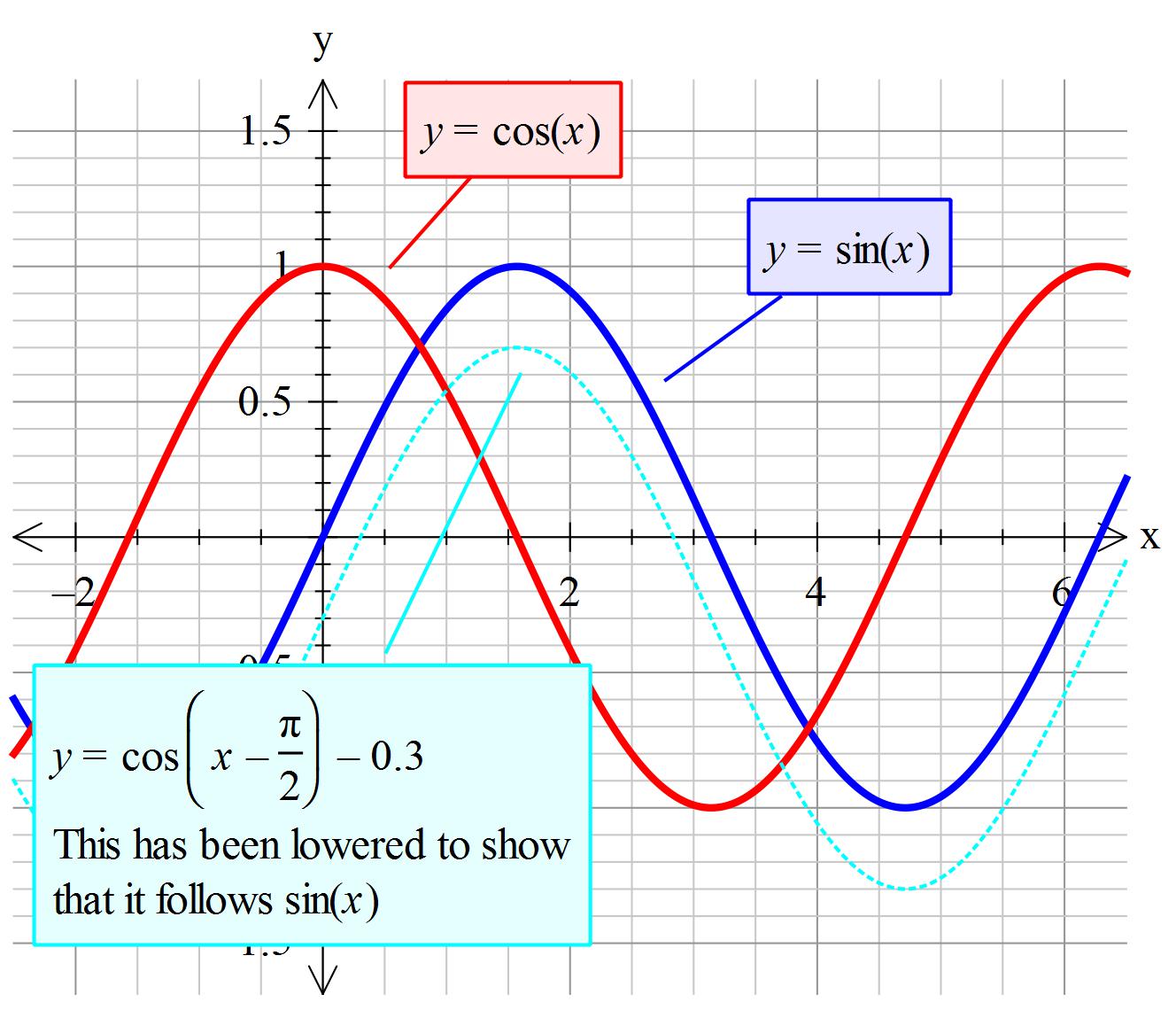



How Do You Prove Cos X Pi 2 Sin X Socratic




Which Function Has The Graph Shown A Y Cosxb Y Sin X C Y Cos X Pi 2 D Y Cosx Brainly Com




Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
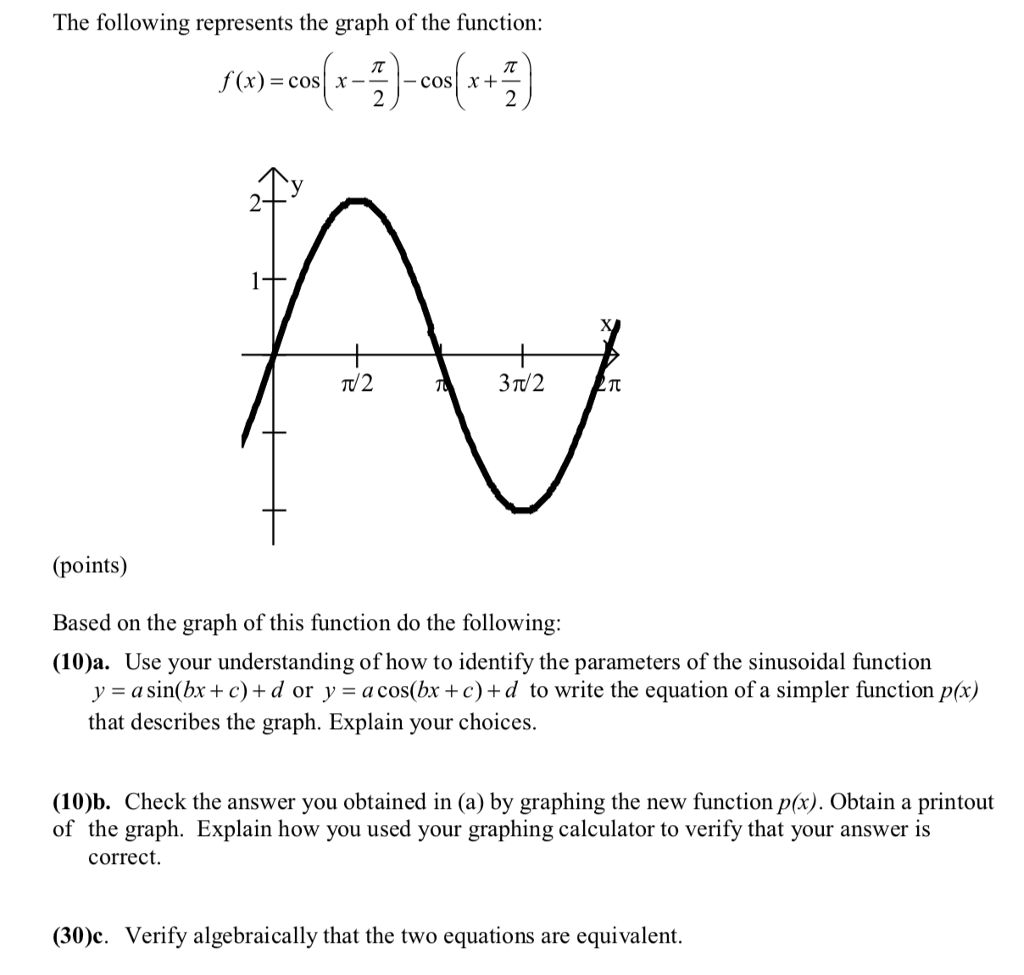



The Following Represents The Graph Of The Function Chegg Com




Graph Of F X Sin X Cos X Youtube



Solved 15 2 Points Scalcet8 3 4 059 0 6 Submissions Used Find All Points On The Graph Of The Function F X 2 Cos X Cos X At Which The Ta Course Hero




Ppt Graphs Of The Sine And Cosine Functions Powerpoint Presentation Free Download Id 4347



2 5 Webassign Answers




Which Function Is Shown On The Graph A F X 1 2 Cos X B F X 1 2 Cos X C F X Brainly Com




Pin On Math



How Do You Graph Y Cosx 3 Socratic




Make A Conjecture Based On The Graph The Graph Is Chegg Com
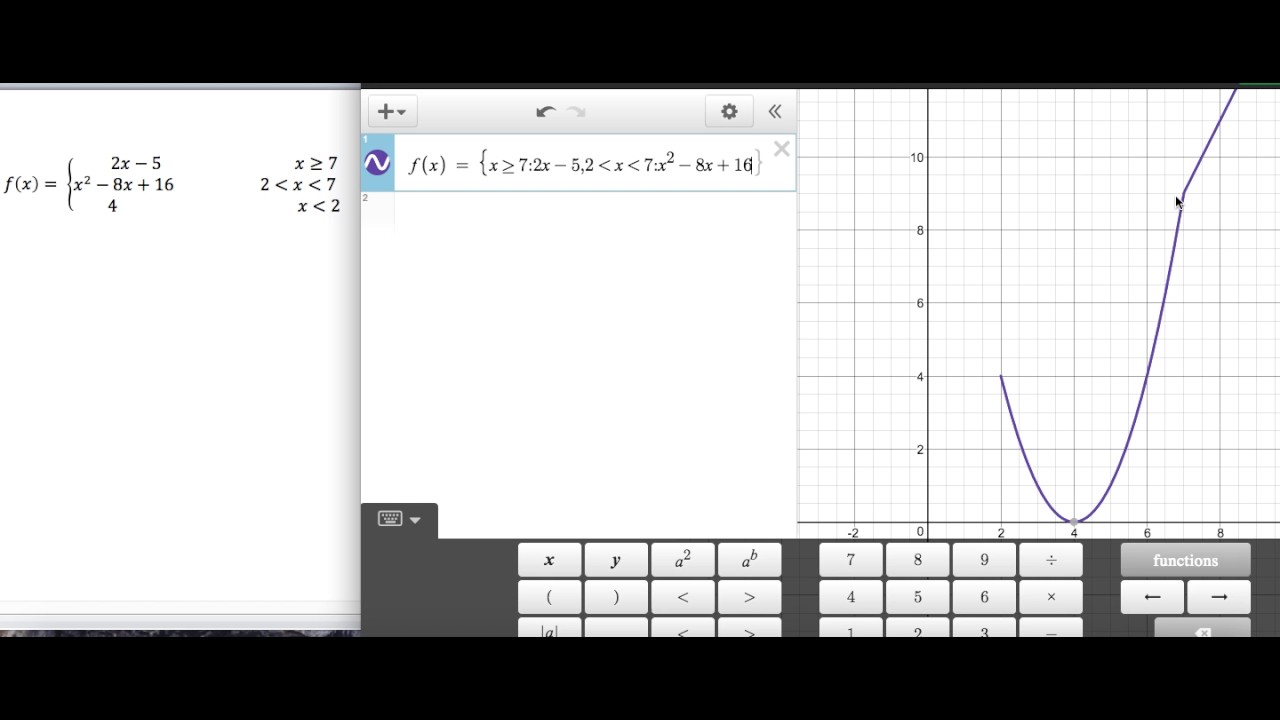



Piecewise Defined Functions College Algebra




Range Of The Function F X Cos 1 X Where Is Fra



2 5 Webassign Answers




If 2 Cos X Sin X 3 Then The Range Of The Function F X Sin X Sqrt3 Cosx In Youtube




Proof Of The Derivative Of Cos X Video Khan Academy




The Range Of Function F X Cos X


